坐标变换对矢量分量的影响

在物理学中，当我们进行坐标变换时，矢量的表示往往也会随之发生变化。这个过程是通过矢量在新坐标系下的分量与原坐标系下的分量之间的关系来描述的。下面我们来详细探讨坐标变换时矢量分量的变化。

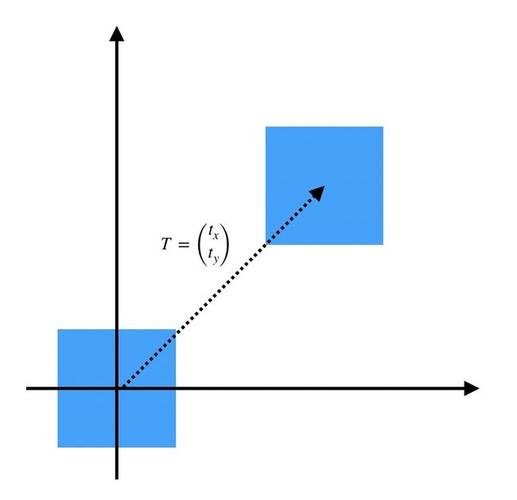
假设原始坐标系下的一个矢量为$\vec{V}$，其在$x, y, z$三个方向上的分量分别为$V_x, V_y, V_z$，在新坐标系下的分量分别为$V_{x'}, V_{y'}, V_{z'}$。坐标变换可以表示为：

$$

\begin{pmatrix}

V_{x'} \\

V_{y'} \\

V_{z'}

\end{pmatrix}

=

\begin{pmatrix}

a & b & c \\

d & e & f \\

g & h & i

\end{pmatrix}

\begin{pmatrix}

V_x \\

V_y \\

V_z

\end{pmatrix}

$$

在坐标变换下，矢量的分量变换遵循以下规律：

在坐标变换下，矢量的方向也会发生变化。原始坐标系下的矢量$\vec{V}$和新坐标系下的矢量$\vec{V'}$之间的关系可以用线性变换矩阵来描述：

$$

\vec{V'} = A \vec{V}

$$

其中$A$是一个线性变换矩阵，它描述了坐标系之间的关系。

坐标变换对矢量分量的影响是一个复杂但可计算的过程，需要逐步分析各个方向的分量变化，并考虑矢量方向的变化。通过适当的数学运算，可以准确描述在不同坐标系下矢量的性质和行为。

《张朝阳的物理课》介绍广相的数学基础

在《张朝阳的物理课》中，广义相对论是一个重要的物理学理论，它描述了引力是时空弯曲形成的，并提出了曲率张量与能动张量的关联性。

广义相对论是爱因斯坦提出的一种描述引力的理论。其基本原理包括：

广义相对论的数学基础主要建立在黎曼几何学和张量分析的基础上。其中，引入了曲率张量、度规张量以及能动张量等概念。数学工具的运用使得我们可以准确描述时空的几何结构和物质的分布。

广义相对论在宇宙学、黑洞物理学、引力波探测等领域都有重要应用。它推动了我们对时空结构和引力的理解，不仅对基础物理学产生深远影响，也在技术和应用领域有着重要意义。

《张朝阳的物理课》对广义相对论的数学基础进行了介绍，帮助读者更好地理解引力是如何塑造时空结构的，并揭示了引力与能量动量之间的密切联系。