张朝阳的物理课巧解屏蔽库伦势，变分法计算氦原子基态能

在量子力学的世界里，氦原子作为最简单的多电子原子，其基态能量的计算一直是物理学家关注的焦点。在《张朝阳的物理课》中，张朝阳教授巧妙地运用变分法，结合屏蔽库伦势的概念，为我们揭示了氦原子基态能量的计算方法。本文将详细介绍这一过程，带领读者领略物理学的魅力。

我们需要了解氦原子的基本结构。氦原子由两个质子和两个电子组成，其电子云分布决定了原子的能量状态。在基态时，两个电子都处于最低能级，且自旋相反，以满足泡利不相容原理。计算氦原子基态能量，就是要找到描述电子云分布的最佳波函数，并计算其对应的能量。

传统的量子力学方法，如哈特里福克方法，虽然能够给出较为准确的能量值，但其计算过程复杂，不易于理解。而变分法作为一种近似方法，通过选择一个试探波函数，并调整其参数，使得计算得到的能量尽可能接近真实值，从而简化计算过程。

在《张朝阳的物理课》中，张教授引入了屏蔽库伦势的概念。由于两个电子之间存在相互作用，一个电子感受到的核电荷会因为另一个电子的存在而减少，这种现象称为屏蔽效应。屏蔽库伦势就是考虑了这种效应的库伦势，它能够更准确地描述电子间的相互作用。

张教授选择了一个简单的试探波函数，它由两个氢原子波函数的乘积构成，并引入一个变分参数来调整波函数的形状。通过变分法，我们可以计算出这个试探波函数对应的能量，并寻找使得能量最小的变分参数值。

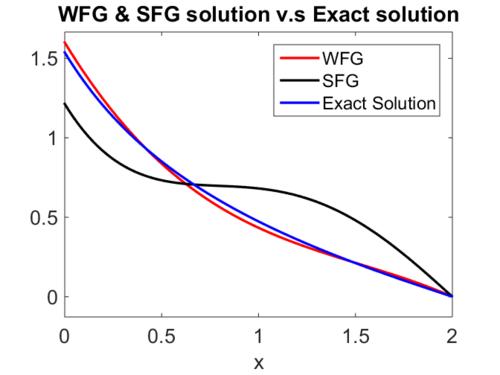
计算过程涉及到复杂的数学运算，但张教授以其深厚的物理学功底，将这一过程讲解得清晰易懂。他首先计算了电子间的库伦相互作用能，然后考虑了屏蔽效应，最后通过变分法找到了最佳的变分参数。

经过计算，张教授得到了氦原子基态能量的近似值，并与实验值进行了比较。结果显示，变分法给出的能量值与实验值非常接近，证明了这种方法的有效性。

通过《张朝阳的物理课》，我们不仅学习到了如何用变分法计算氦原子基态能量，更重要的是，我们体会到了物理学中近似方法的巧妙和实用。变分法虽然是一种近似方法，但在处理复杂系统时，它能够提供一种简单而有效的解决方案。

总结来说，张朝阳教授在《张朝阳的物理课》中巧妙地运用变分法和屏蔽库伦势，为我们展示了氦原子基态能量的计算过程。这不仅是一次物理知识的传授，更是一次思维方式的启迪。通过这样的课程，我们能够更加深刻地理解量子力学的奥妙，激发对物理学的热爱和探索欲望。