正方体展开图，探索空间几何的奇妙之旅

在我们的日常生活中，几何图形无处不在，从建筑设计到包装设计，从艺术创作到数学研究，几何图形以其独特的美感和实用性，成为了连接艺术与科学的桥梁，在众多几何图形中，正方体作为一种基本的空间几何体，其独特的性质及其展开图的应用，在教育、设计乃至科学研究领域都有着广泛的应用，本文将带领大家走进正方体的世界，探索正方体及其展开图的魅力所在。

正方体的基础知识

正方体是一种特殊的长方体，它有六个面且每个面都是相等的正方形，这种几何体拥有许多有趣的性质：

对称性：正方体具有高度的对称性，无论是在平面内还是三维空间中，正方体都具有多个对称轴和平面对称性。

顶点与边的关系：正方体有8个顶点、12条边和6个面，每个顶点都是三条边的交汇点，每条边连接两个不同的顶点。

体积和表面积计算公式：给定正方体边长为a，则正方体的体积V=a³，表面积S=6a²。

正方体展开图的认识

正方体展开图是指将正方体表面的六个正方形按照一定的规律展开成平面图形，了解不同形式的正方体展开图对于学习空间几何、培养空间想象力以及解决实际问题都有着重要的意义。

1. 展开图的基本类型

正方体展开图有多种可能的形式，但并不是所有的组合都能构成有效的正方体展开图，下面列举了几种常见的有效正方体展开图形式：

1-4-1型：这是最常见的展开方式之一，由中间四个相连的正方形构成主体，两侧各有一个正方形。

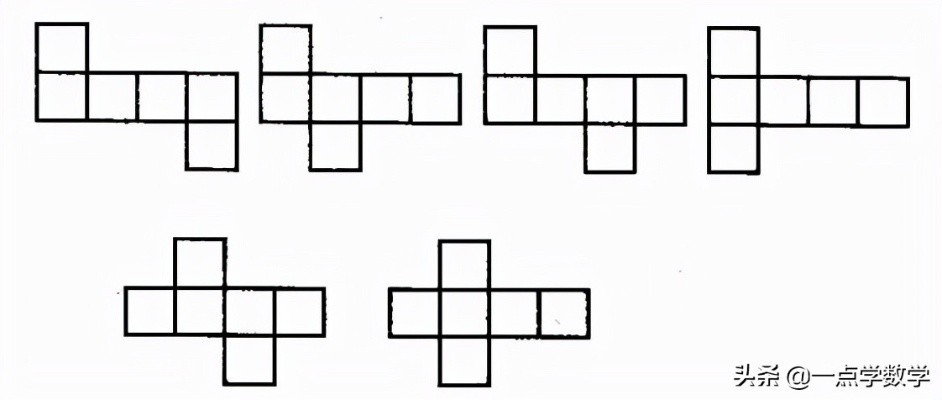
2-2-2型：将正方体分成三列，每列包含两个正方形。

3-3型：正方体被分为两行，每行包含三个正方形。

2. 如何判断展开图的有效性

要判断一个展开图是否能够折叠回一个完整的正方体，可以遵循以下几点原则：

- 确保所有正方形相连。

- 每个正方形只能直接或间接地与另外五个正方形相邻。

- 避免出现“田”字形结构（即不能有四个正方形围成一个小正方形）。

通过这些简单的规则，我们可以快速判断出哪些展开图是有效的。

正方体展开图的应用实例

正方体展开图不仅在数学教学中占有重要地位，而且在现实生活中也有着广泛的应用：

1. 教育中的应用

帮助学生理解空间概念：通过制作正方体模型或绘制展开图，可以帮助学生直观地理解三维空间中的几何关系。

提高空间想象力：引导学生尝试不同的展开方式，鼓励他们思考如何将平面图形折叠成三维物体。

2. 设计领域的应用

包装设计：利用正方体展开图原理设计各种形状的盒子或包装容器。

艺术品创作：结合不同颜色、图案和材质的正方形纸片，艺术家们可以创造出极具创意的作品。

正方体及其展开图不仅是几何学中的重要内容，也是连接艺术与科学的纽带，通过本文的介绍，希望能够激发读者对于几何图形的好奇心，进一步探索其中蕴含的无限奥秘，无论是对于学生来说，还是对于设计师、艺术家而言，掌握正方体展开图的知识都将大有益处。

通过这篇文章，我们不仅介绍了正方体的基础知识及其展开图的相关内容，还探讨了它们在不同领域中的应用，希望能为广大读者带来启发和帮助。