揭秘对数函数的奇妙世界，探索对数函数的核心性质

在数学的广阔天地里，有一种函数以其独特的魅力吸引着无数探索者，它就是对数函数，无论是在高中数学课堂还是高等数学研究中，对数函数都是一个不可或缺的话题，我们就来一起揭开对数函数神秘的面纱，深入探索它的核心性质及其背后的数学之美。

什么是对数函数？

对数函数是基于指数函数的一种逆运算，如果我们用指数的形式表示为 \(a^x = y\)，那么其对数形式则可以写作 \(x = \log_a{y}\)，这里，\(a\) 称为基础（base），且 \(a > 0\)、\(a \neq 1\)；\(x\) 是以 \(a\) 为底 \(y\) 的对数，对数函数的一般形式可以表示为 \(f(x) = \log_a{x}\)，\(x > 0\)。

对数函数的基本性质

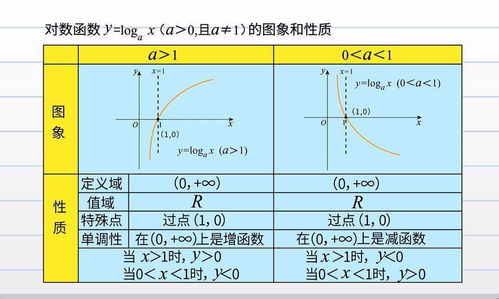
1、定义域与值域：由于 \(a^x > 0\) 对所有的 \(x\) 成立，因此对数函数 \(f(x) = \log_a{x}\) 的定义域是所有正实数，即 \((0, +\infty)\)，而对于 \(a > 1\) 和 \(0 < a < 1\) 的两种情况，其值域均为 \((-∞, +∞)\)。

2、单调性：当 \(a > 1\) 时，对数函数 \(f(x) = \log_a{x}\) 在其定义域内是严格增函数；而当 \(0 < a < 1\) 时，则是严格减函数。

3、零点：对于所有 \(a > 0\) 且 \(a \neq 1\)，函数 \(f(x) = \log_a{x}\) 的零点总是位于 \(x = 1\) 处，因为对任何 \(a\) 都有 \(a^0 = 1\)。

4、奇偶性与周期性：对数函数既不是奇函数也不是偶函数，并且没有周期性。

5、基本公式：

换底公式：\(\log_a{b} = \frac{\log_c{b}}{\log_c{a}}\)，\(c > 0\) 且 \(c \neq 1\)。

积的对数：\(\log_a{xy} = \log_a{x} + \log_a{y}\)。

商的对数：\(\log_a{\frac{x}{y}} = \log_a{x} - \log_a{y}\)。

幂的对数：\(\log_a{x^n} = n\log_a{x}\)。

根的对数：\(\log_a{\sqrt[n]{x}} = \frac{1}{n}\log_a{x}\)。

6、特殊值：值得注意的是，自然对数函数（以 \(e\) 为底）具有特殊的性质，\(\ln(e) = 1\)，并且在其定义域内处处连续且可导。

对数函数的应用实例

对数函数不仅仅停留在理论层面，在实际应用中也起着重要作用。

生物学中的 pH 值：pH 值是衡量溶液酸碱性强弱的指标，通过计算 \(-\log_{10}[H^+]\) 得到，\([H^+]\) 表示溶液中氢离子浓度。

经济学中的需求函数：对数函数可以用来建模商品价格与需求量之间的关系，帮助经济学家预测市场行为。

计算机科学中的算法效率分析：对数时间复杂度 \(\mathcal{O}(\log n)\) 表示随着输入规模的增加，所需时间增长缓慢，常见于排序和搜索算法中。

通过对数函数的学习，我们不仅可以深入理解数学理论本身，还能感受到数学在现实生活中的广泛应用，希望本文能够帮助大家更好地掌握对数函数的知识，激发学习兴趣，进一步探索数学的魅力！